Topological states have shown prospect for bringing topological robustness into various applications and have been widely investigated in different physical systems and diverse types of lattice structures.
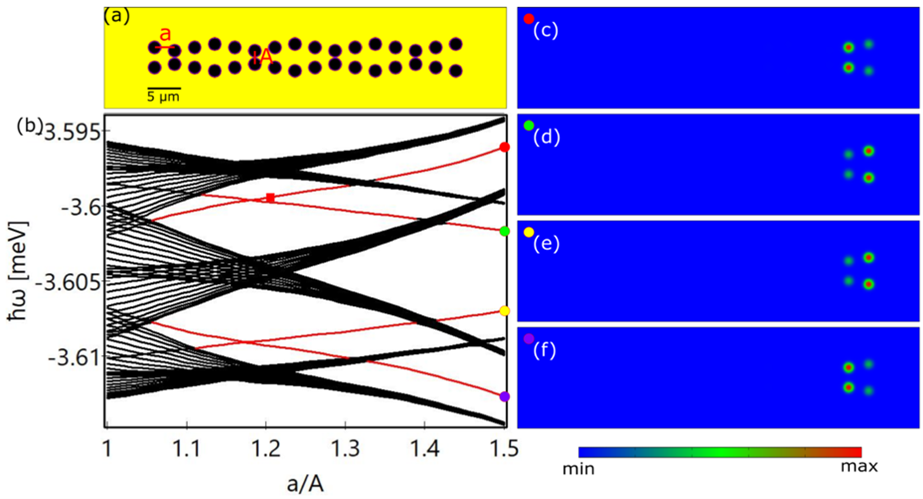
Recently, Tobias Schneider and co-authors proposed a new type of lattice that contains two coupled cosinusoidal modulated potential chains (double-wave chains) as represented in (a) for the study of topological states in a planar semiconductor microcavity system with polaritonic excitations. In such double-wave chains, different kinds of edge states [see (c)-(f)] that reside in the energy band gaps [see (b)], which are topologically nontrivial, are been found. Thanks to the strong nonlinearity of microcavity polaritons, which are light-matter hybrid quasiparticles, more than one of these edge eigenstates and their combination can be stabilized at the same excitation, known as multistability. Interestingly, the nonlinearity can even give rise to a new type of edge state that goes beyond the linear eigen spectrum.
The authors also report the regular stacking of multiple identical such double-wave chains into a 2D structure, resulting in multiple Su-Schrieffer-Heeger (SSH) chains in the direction perpendicular to the double-wave chains. The topology of the nontrivial double-wave chain and the nontrivial SSH chains leads to the formation of corner states inside an energy band gap (i.e., higher-order topological insulators). Multistable corner states can occur under the same excitation condition due to the nonlinearity, which offers potential applications in for example all-optical switching. The topological structure and the topological states the authors introduced are of very general nature and can be realized in different physical implementations.
More details can be found here in the original article: https://doi.org/10.1515/nanoph-2023-0556
Authors: Tobias Schneider, Wenlong Gao, Thomas Zentgraf, Stefan Schumacher and Xuekai Ma